Nasceu em Pisa, em 15 de Fevereiro de 1564, era filho de Vincenzo Galilei (1520-1591), um estudioso de música e Giulia Ammannati (1538-1620). Estudou na Universidade de Pisa, onde ocupou a cadeira de matemática de 1589 a 1592. Em seguida, foi nomeado para a cadeira de matemática na Universidade de Pádua, onde permaneceu até 1610. Em Pádua, ele realizou estudos e experiências em mecânica. Em 1610, foi nomeado matemático e filósofo pelo Grão Duque da Toscana. Ingressou na Academia dos Linces (em Roma, 1611). Simpatizante e defensor da teoria heliocêntrica de Copérnico, Galileu foi denunciado, em 1614, pelo Padre Tommaso Caccini (1574-1648), que considerou os seus argumentos sobre o movimento da Terra perigosos e contrários aos ensinamentos das escrituras sagradas. Após um julgamento longo e injusto Galileu foi condenado a renunciar publicamente as suas ideias. Os livros de Galileu foram incluídos no Index, censurados e proibidos. Reza a lenda que, ao sair do tribunal após sua condenação, disse uma frase célebre: "Eppur si muove!", ou seja, "contudo, ela se move", referindo-se à Terra. Galileu conseguiu comutar a pena de prisão à pena de confinamento, primeiro no palácio do embaixador do Grão-duque da Toscana em Roma, depois na casa do arcebispo Piccolomini em Siena e mais tarde na sua própria casa de campo em Arcetri, onde veio a falecer, aos 78 anos de idade, em 8 de janeiro de 1642.

Talvez o grande “pecado” de Galileu foi questionar publicamente dois grandes pilares da filosofia cristã: o homem como centro do universo e a física de Aristóteles como modelo para a ciência. Seu método científico é, sem dúvida o grande legado que o mestre deixou para humanidade. É considerado, por conta disso, o “pai da ciência moderna”. Em sua última obra “Discursos Referentes a Duas Novas Ciências a Respeito da Mecânica e dos Movimentos Locais”, o pensador italiano demonstrou, ao contrário da tradição aristotélica, que o peso de um corpo não exerce influência na velocidade da queda livre e, de quebra, enunciou a lei da queda dos corpos no vácuo: o espaço percorrido por um corpo em queda livre é diretamente proporcional ao quadrado do tempo levado para percorrer este espaço. Isso mesmo, a função que descreve a posição “s” do corpo em relação ao tempo “t” é uma função quadrática.

Fig.1 - Galileu enfrentando a Inquisição Romana

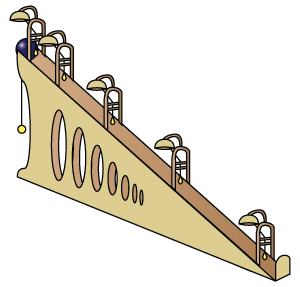
   Não há documentos que provem, mas acredita-se que para chegar à lei enunciada, o grande mestre realizou um experimento fazendo uso de um instrumento similar ao da figura a seguir.

Fig.2 - ilustração do instrumento exposto no Instituto e Museu da História da Ciência, em Florença (Itália)	Fig.3 - detalhe do sino

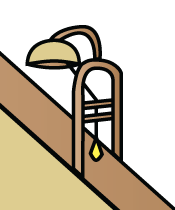
   O experimento consiste em liberar uma pequena bola da extremidade superior do plano (fig.2), ao mesmo tempo em que um pêndulo suspenso é colocado em movimento. A cada movimento do pêndulo, a bola atinge um dos sinos pequenos (fig.3) colocados ao longo do plano inclinado. As distâncias entre os sinos (que expressam os deslocamentos da bolinha em cada unidade de tempo – metade do período do pêndulo) formam uma sequência de números ímpares. Uma animação desta pode ser vista clicando no link http://brunelleschi.imss.fi.it/museum/emulti.asp?player=wmv&codice=500045&banda=h. Quer saber mais? Resolva os problemas 1, 2 e 3 deste módulo. A escolha desses problemas para compor o nosso módulo não é mera coincidência, pode ter certeza!

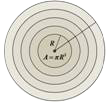
   Podemos observar diversas situações do cotidiano ou da ciência em que a função quadrática é bastante útil para modelar ou resolver um problema.

   Em geometria, por exemplo, a área de um círculo é proporcional ao quadrado do comprimento do seu raio e a área do quadrado é igual ao comprimento do seu lado ao quadrado.

   Além dos exemplos anteriores, as áreas de outras superfícies geométricas também são proporcionais à medida de um de seus elementos lineares: a superfície esférica é, por exemplo, proporcional ao quadrado do comprimento do raio da esfera subtendida ($A = 4\pi{R}^{2}$) e a área do cubo é proporcional ao comprimento da aresta ao quadrado ($A = 6l^{2}$).

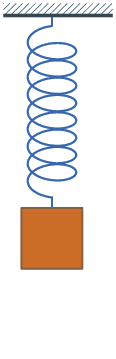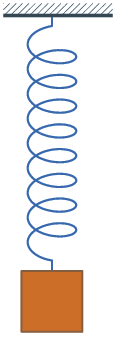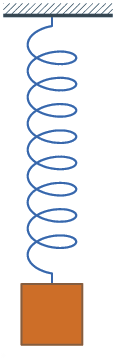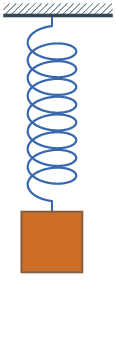
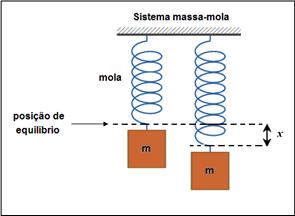
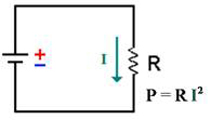
   Na disciplina de física, você já deve ter ouvido falar de equação horária de um corpo em queda livre, energia potencial elástica de uma mola, movimento uniformemente acelerado (a queda livre é um caso particular deste tipo de movimento), energia cinética, etc. A função quadrática é bastante útil nesses contextos!

Energia potencial elástica de uma mola    Se considerarmos que uma mola apresenta comportamento ideal, ou seja, que toda energia que ela recebe para se deformar ela realmente armazena, podemos escrever que a energia potencial $E_{el}$ acumulada nessa mola vale: $E_{el} = \displaystyle\frac{kx^{2}}{2}$ sendo $x$ a deformação (contração ou distensão) sofrida pela mola e $k$ a constante elástica da mola.

Energia cinética
	A variação de energia cinética é a quantidade de trabalho que teve que ser realizado sobre um objeto para modificar a sua velocidade (seja a partir do repouso - velocidade zero - seja a partir de uma velocidade inicial). Para um objeto de massa $m$ a uma velocidade $v$ a sua energia cinética, em um instante de tempo, é calculada por $E_{c} = \displaystyle\frac{1}{2}mv^{2}$.

Potência

A energia elétrica pode ser convertida em energia térmica, mecânica, sonora e luminosa. A potência elétrica $P$ (em watt) dissipada ou que está sendo convertida em calor por um resistor $R$ (em ohm) é dada pela fórmula $P = R\,I^{2}$, em que $I$ é a corrente elétrica que atravessa o resistor $R$.

Foto de resistores

   Agora é com você, consulte seus professores e encontre outras equações que exprimem uma grandeza como função quadrática de outra.

   Com base nas atividades do módulo, observamos que uma função quadrática $f : $ IR $ \to $ IR tem a seguinte propriedade:

• a sequência $y_{n} = f(x_{n})$ formará uma progressão aritmética de segunda ordem, qualquer que seja a progressão aritmética $(x_{n})_{n \in \mathbb{N}}$, não degenerada no domínio da função.

   Suponha agora que tenhamos uma função $f : $ IR $ \to $ IR que satisfaz a propriedade acima, será que podemos afirmar que $f$ é uma função quadrática? Vimos que a resposta para esta questão, se considerarmos o universo das funções contínuas, é “sim”. Ficamos devendo a demonstração do resultado. Pois é, agora não devemos mais nada!

Teorema (Caracterização das Funções Quadráticas.)

   Se $f : $ IR $ \to $ IR é uma função contínua que transforma toda progressão aritmética não-constante $x_{1}$, $x_{2}$, ..., $x_{n}$, ... numa progressão aritmética de segunda ordem não-degenerada $y_{1} = f(x_{1})$, $y_{2} = f(x_{2})$, ..., $y_{n} = f(x_{n})$, ..., então $f$ é uma função quadrática.

Demonstração: Seja $f : $ IR $ \to $ IR uma função contínua com a propriedade de transformar toda P.A. não-constante numa P.A. de segunda ordem não-degenerada. Substituindo $f(x)$ por $g(x) = f(x) - f(0)$, vemos que $g$ tem as mesmas propriedades de $f$ e mais a propriedade adicional de que $g(0) = 0$.

   Considerando a progressão aritmética 1, 2, 3, 4, 5, ..., vemos que os valores $g(1)$, $g(2)$, ..., $g(n)$, ... formam uma P.A. de segunda ordem não-degenerada. Logo existem constantes $a \neq 0$ e $b$ tais que

para todo $n \in \mathbb{N}$. (Deveria ser $g(n) = an^{2} + bn + c$ porém $g(0) = 0$.)

   Em seguida, fixemos arbitrariamente um número $p \in \mathbb{N}$ e consideremos a progressão aritmética

   De modo análogo, concluímos que existem $a' \neq 0$ e $b'$ tais que

para todo $n \in \mathbb{N}$, temos:

   Portanto as funções quadráticas

coincidem para todo $x = n \in \mathbb{N}$. Como vimos no início deste capítulo, isto obriga a $a = a'p^{2}$ e $b = b'p$, ou seja, $a' = \displaystyle\frac{a}{p^{2}}$, $b' = \displaystyle\frac{b}{p}$. Logo, para quaisquer números naturais $n$ e $p$ vale:

   Vemos então que as funções contínuas $g(x)$ e $ax^{2} + bx$ são tais que $g(r) = ar^{2} + br$ para todo número racional positivo $r = \displaystyle\frac{n}{p}$. Segue-se que $g(x) = ax^{2} + bx$ para todo número real positivo $x$. De modo análogo, considerando a P.A. -1, -2, -3, ..., concluiríamos que $g(x) = a^{2} + bx$ para todo $x \leq 0$. Logo, pondo $f(0) = c$, temos $f(x) = g(x) + c$, ou seja,

para todo $x \in $ IR.

Boyer, C. B. (1949) The History of the Calculus and its Conceptual Development. New York: Dover Publications Inc.

Hughes-Hallett, D., Gleason, A. M., Lock, P.  F., Flath, D. E. et al. (1999) Cálculo e Aplicações. São Paulo: Editora Edgard Blücher LTDA.

Lima, E.L., Carvalho, P. C. P., Wagner, E. & Morgado, A. C. (2001) A Matemática do Ensino Médio. Coleção do Professor de Matemática. V. 1. Rio de Janeiro: Sociedade Brasileira de Matemática.

Instituto e Museu da História da Ciência (Florença, Itália). Video que apresenta uma simulação da suposta experiência  realizada por Galileu de uma bolinha descendo uma rampa inclinada.
Disponível em  http://brunelleschi.imss.fi.it/museum/emulti.asp?player=wmv&codice=500045&banda=h.
Acesso em dezembro de 2009.